Discussion Session: Inhomogeneous electronic states in superconductors

Suggested question : How to disentangle the unavoidable atomic level inhomogeneity of real materials from the electronic inhomogeneity ?

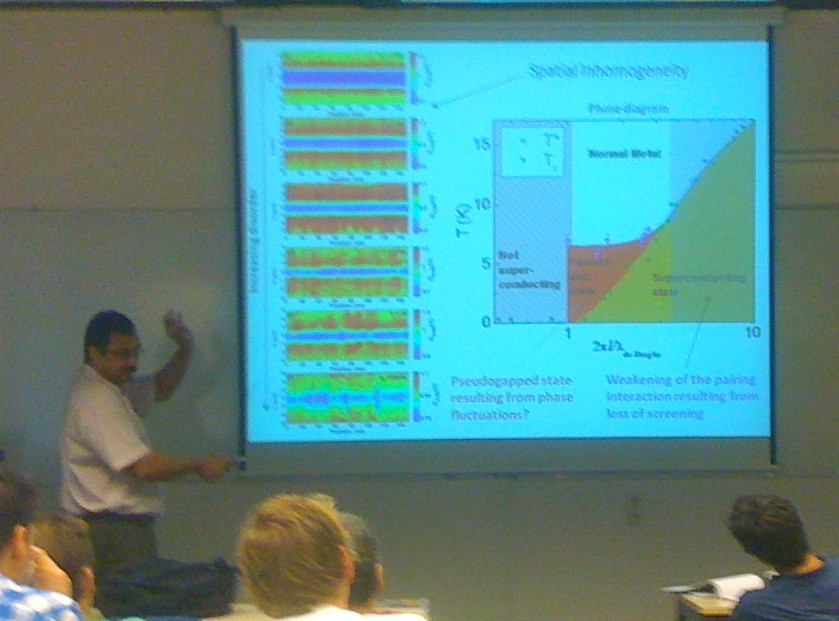
The first debated question was the role of fractality in the spontaneously emergent spatial inhomogeneities observed in highly disordered superconductors. According to the results of numerical simulations reported by Prof. Trivedi, this fractality holds only close to the metal-insulator transition in the non-interacting particles Anderson localization transition. However, deeper in the insulating state where the superconductor-insulator transition (SIT) takes place, once the pairing interaction is switched on, this fractal character of the wave functions does not show up in the u and v BCS operators, possibly because the wave functions are now too strongly localized. Dr. Feigel’man remarked that this could also be a side effect of the non perturbative implementation of the pairing potential in these calculationsand stressed that, in the fractal theory of the SIT, the spatial variations of the order parameter are expected to show the fractal behaviour only in the limited range of distances because at large scales local pairing amplitude relies on the participation of several localized wave-functions while no fractal structure is expected at distances less than a mean free path of electrons. This is also true for any other physical observable which varies in real space. This range of distances significant for realistic physical systems with small T_c/E_F ratio and short mean free path but shrinks as T_c/E_F →1 as is the case for numerical simulations. Moreover, it has been emphasized that the fractal character of the wave-functions at the mobility edge does not lead to the SIT, but rather to an enhancement of the pairing interaction. The superconducting properties disappear for higher disorder when the mean level spacing is much higher than the superconducting gap. The main role of fractality is to give broad spatial distribution of the pairing amplitude of electrons in a single localized state. In conclusion, no exotic physical length scale appears in the theory, beside the usual superconducting coherence length and the localization length. There seems to be no contradiction between numerical results of Prof. Trivedi and analytical theory.

The second discussed issue was the possibility that inhomogeneities might explain the puzzles observed by Prof. Raychaudhuri on NbN films. Namely, for several disordered films, the transport and Hall effect measurements at high temperatures give the value of (k_Fl) that is much smaller than unity. In this situation one expects that these materials become insulators at low temperatures. However, in case of NbN films, the resistance remains finite when extrapolated to zero temperature. One possible explanation of this disagreement is that the measured conductivity is dominated by a small percolating volume of the film. Another explanation attributes it to a significant thermal dependence of the electronic density which is only known at room temperature.

Although disorder driven electronic segregations in nominally homogeneous materials seem to become an established concept supported by theoretical calculations and experimental observations, the usual dichotomy between granular and homogeneously disordered systems is still extensively emphasized in most of the presentations which show the famous sets of R(T) curves in Ga and Bi. Although this systematic opposition might be misleading, the general opinion is that it should be continued to be discussed because, despite being an oversimplification, it helps non-specialists to clarify a complex SIT landscape.

Prepared by Lev Ioffe and Claude Chapelier

Vladimir Manucharyan: Superinductance: engineering and characterization.

He reports about large inductances realized with series arrays of Josephson-junctions and means to characterize them. The experimental techniques used may very well be useful to characterize large inductances realized with highly disordered superconductors.

He starts by showing a catalogue of commercially available inductors (Coilcraft) and shows that they always have a failure mode, which implies that the impedance will never exceed the quantum resistance. This is due to the finestructure constant, which he blames to be too small.

Large inductance circuits are useful for 1; enhanced coupling in QED systems 2; electrical current metrology with Bloch oscillations in JJ’s. 3; Topologically protected quantum states in network of JJ’s. 4; eliminate flux noise in flux qubits (cf. Kerman’s poster).

One could use disordered superconductors, which requires a careful choice of controllable material and of which as of today the electrodynamics is poorly understood. Instead the ‘workhorse’ of superconducting quantum-engineering is used, the Al tunneljunction. A chain of JJ’s can act as an inductor, even tunable because of its dependence on the bias current.

In designing the most useful inductor one needs to consider a long list of possible failures, which are not a priori trivially known. Therefore it is very important to be able to measure and characterize the inductor thoroughly.

He describes 2 methods, of which one of them is easy to implement for highly disordered superconductors. The other one requires integration in a high-Q qubit structure, which is less readily available. The outcome is that coherent quantum phase slip is resolved down to 100 kHz, which connects his presentation to the first two of the workshop by Hans Mooij and Oleg Astafiev, although the QPS is realized in a series array of JJ’s (like by Pop, .., Guichard et al from Grenoble. )

The speaker believes that the highly disordered superconductors are potentially very useful for compact high-Q resonators coupled to semiconductor quantum dots, Rydberg atoms on a chip, polar molecules, or anything with a small dipole moment and a long life time.

Blogged by Teun Klapwijk

Thierry Klein: Superconducting properties of boron-doped silicon

Thierry Klein started off with review of superconductivity in covalent bonded materials and row IV systems. He gave example of fullerenes and Si-Clathrates. He then discussed the reasonably recent example of superconductivity in diamond. He motivated that it exected that the el-phonon coupling constant could be as big as 280 meV. He gave a naive estimate forecast of a Tc based on this el-phonon coupling for this sample of 200K.

Was discovered by Ekimov et al. in 2004. It is believed that superconductivity occurs in an sp3 band.

It appears with B doping at the onset of the metal-insulator transition. Tc is NOT 200K in this compound; it is limited to ~10K presumably due to the low charge carrier density.

Diamond superconducting films can also be grown by plasma assisted CVD, which appeared to this blogger to have a max Tc in these films of about 3K. It has also been discovered intercalated graphite has Tc around 11K in 2005. In 2007 they discovered superconductivity in B doped Si.

Gas immersion laser doping is done to increase B concentration of Si. Apparently it is not possible to doped to high enough concentrations in a melt. The necessary concentrations of B are above the solubility limit of B in Si. To this blogger they blast and melt the surface of a Si with a laser. The surface recrystallize under some atmosphere of B which is incident. They can make highly doped B doped Si layer.

At 1% Boron concentrations the transition starts and rises linear. This is difference than diamond, where Tc comes up with an exponent of ~ 0.5. The superconducting transition doesn't coincide with the MIT. That is at much lower concentrations. The max Tc looks to be about 0.5K. The superconductivity in this system is extreme type II. Unlike the case of diamond where k_Fl is about 1, k_Fl in this system is about 10.

Calculations can postdict the superconductivity reasonably, but there is uncertainty about mu* (as there is always). But with a mu* of about 0.14 (typical for metals), they can describe Tc.

Blogged by Peter Armitage

Michael Gershenson: Magnetic-field driven phase transitions in unconventional Josephson arrays

Michael started off by reminding us of the Bosonic model of superconductor-insulator transition (SIT).

In this model as applied to Josephson Junction arrays, there is charge-flux duality. Can be described by a Hamiltonian with Josephson couplings between scing island and charging energies for the islands.

In the regime where Ec
There are a number of possible complications in the simple arrays including random charge, and Josephson energies, and flux noise.

They have endeavored to overcome these issues by making JJ arrays with a large number of nearest-neighbor islands. These are arrays where there is a supercell of many tightly connected neighbors. This supercell is connected to its neighboring supercells, by cells that have less interconnects. With these array they can explore of a wide range of JJ parameters and an effective Ej/Ec created which is enhanced over the bare value by factor of N^2.

Michael 1st presented data for array without ground planes and then for arrays conducting ground plane. They found multiple SIT (due to commensurate effects) over a wide range of critical resistances R ~ 3-20 k were observed. "Metallic" phases with very low (typically < 100 mK) characteristic energies were found.

SIT observed at low “critical” Rcr ~ few ohms resemble the “dirty boson” SIT however the duality is lacking for the transitions observed at larger Rcr . On the “insulating” side of the SIT, the R(T) dependences can be fitted with the Arrhenius law R(T)~exp(T0/T), where kBT0 is close to the “Coulomb” gap 2eV* (V* is the offset voltage across the whole array). Michael speculated that this may be a signature of some collective process and/or macroscopic inhomogeneity. The threshold for quasiparticle generation at high bias currents is surprisingly universal for samples with vastly different zero-bias resistances and that this power scales with the array area.

Blogged by Peter Armitage

Wei Liu : Dynamical study of phase fluctuations and their critical slowing down in amorphous superconducting films

Wei Liu introduced her talk by a description of the superconducting transition as seen in the thermal dependance of the resistance. She divided the curve into three main parts: a normal state behavior at high temperature, a superconducting fluctuations region when the curve bends down at the transition and a superconducting state characterized by a zero resistance. She emphazised that the critical region of the transition is divided into an amplitude fluctuation region at the beginning of the downturn of the curve and a phase fluctuation region at lower temperature. In the phase fluctuation region, free vortices are thermally generated down to the Berezinsky–Kosterlitz–Thouless (BKT) transition where these fluctuations are frozen out. The speaker described different signatures of this BKT transition: a universal resistance curve [P. Minnhagen (1987)] and the non linear I-V characteristic [K. Epstein (1982)].The critical temperature of the BKT transition is theoretically signalled by a jump in the exponent of this charactreristic (not seen in transport measurements as far as the blogger knows). A related universal jump has indeed been seen in the damping rate of a torsion oscillator immersed inHe3/He4 mixtures. The method used by Wei Liu is based on the frequency dependance of the superfluid stifness. Although it was not the premature end of her talk, she immediately anticipated her conclusions: the microwave complex conductivity can characterize two-dimensionnal quantum systems by providing an experimental signature of the superfluid stifness. She observed that the dynamic slows down at the transition.

The experiment relies on the Corbino geometry of the sample which allows a broadband spectrometric study (100 MHz-40 GHz with 1Hz resolution). The measurement consists in recording, with a network analyser, the microwave reflexion of a line ended by the sample cooled down to 300 mK. Both the real and imaginary components of the complex impedance can thus be obtained.

The sample was a 30 nm thick amorphous Indium oxide film with a sheet resistance below 1500 Ohms. An Azlamazov-Larkin paraconductivity analysis of the thermal dependance of the resistance gives a superconducting temperature sligthly below 3 K.

Weil Liu showed the real and imaginary part of the conductance of this film as a function of frequency for different temperatures. In the real conductance, the spectral weight moves to lower frequency as the temperature is decreased. In the supercondsucting state, a gap in the frequency opens and a delta function peak appears at zero frequency as expected for a superconductor with zero DC resistance. The plot of the logarithm of the imaginary conductance shows a linear behavior whose slope continuously changes from a positive value at high temperature to a negative one at low temperature. This imaginary component times the frequency is a direct measure of the energy scale of the superfluid stiffness. The latter becomes frequency dependent above T_BKT (approximately 2.3K) and while its value should be four times T_BKT at this temperature (according to BKT theory), the speaker rather estimates it around 12 K. However, the audience found that there was not such a discrepancy between theory and measurements, taking into account the width of the experimental curves.

The real part of the conductance was also shown for different temperature and a peak above T_BKT could be observed that shifts to even higher temperature when the AC frequency is increased. This peak unveils the superfluid density.

The last part of the talk consisted in a scaling analysis of the phase and the amplitude of the complex impedance. Both quantities could be rescaled on universal curves for a significant range of temperature above the transition. This analysis allowed Wei Liu to extract a characteristic relaxation frequency which decreases rapidly above T_BKT. Such an observation is consistent with a vortex activation scenario. However the blogger did not understand whether the extracted vortex core energy was in agreement or not with BCS theory.

During the discussion, the validity of the BKT interpretation of the data in such a disordered superconductor was questionned. Indeed, one expects the vortex to be pinned. It was recognized that edge pinning was irrelevant because of the Corbino geometry. However, internal pinning could be detrimental. Whether the short length scales probed by these high frequency measurements allows disregarding pinning remains an open question.

Blogged by Claude Chapelier

Discussion group 3: Superconductor-insulator transition: new and old systems

Suggested question: identify experimental tests for the latest developments in the theory of the SIT

Experiments suggested to check recent theories of S-I transition:

1) RF stimulation of activated conductance. Can be used to probe the nature of insulating state which contains (according to theory of Feigelman, Ioffe, Mezard) energy threshold for delocalized excitation, ω_d(g) which vanishes when coupling constant g approaches the critical point g_c RF excitation with frequency ω which is a bit above ω_d may lead to strong increase of conductivity due to specific excitation

of mobile excitations without much heating of the sample.

2) Mapping of supercurrent distribution. According to the theory, close to SIT supercurrent is distributed very inhomogeneously along the sample. It would be important to measure distribution of supercurrents experimentally. Possible methods could include, for example, magnetic AFM or magnetic-field-sensitive NV-centers in diamond, both methods being able to measure magnetic field produced by super-current with a good spatial resolution.

3) Spatial correlation of peak heights and gap widths.

More extensive STM studies are needed to investigate correlation functions of the spatial inhomogeneities of the superconducting state. The spatial evolution of the gap and coherence peak height correlation functions as a function of disorder would be of great interest for understanding how disorder transforms superconductors into insulators.

4) Fate of pseudogap while moving away from SIT ?

According to theoretical description of strongly disordered superconductors, the size of pseudogap is expected to decrease while switching to less disordered samples. Thus it would be important to study if pseudogap features (e.g. seen in InOx near S-I transition) are diminished for less disordered samples, with higher Tc values (like ones used in the phase slip experiment by Oleg Astafiev, or in high-frequency measurements reported Peter Armitage ).

Prepared by B.Sacepe and M. Feigel’man

Discussion Session I Summary: Quantum Phase slips

The discussion was mostly under the sign of the recent report of Oleg
Astafiev concerning the realization of phase-slip qubit with InO nanowires.
It was noted that a number of features in these devices do not correspond to
usual assumptions about what is good and what is bad for big values of
phase-slip amplitude. Big resistance per square in combination with
significant Tc is certainly thought to be needed for the effect. However,
the issue that required discussion is relatively big width and height of
the wires that by factors exceed coherence length expected for the material.
Another issue concerned the effect of uncompensated charged impurities
readily available in insulating subtrate. The charge induced by these
impurities could lead to a total compensation of the phase-slip magnitude.

It has been noted that a phase-slip in a wire that is wider than coherence
length can be seen as a tunneling of Abrikosov vorthex across the wire. The
fact that the tunneling amplitude is appreciable means that such a vorthex
bears a relatively small energy, perhaps at the scale of quasiparticle
energy, and can be regarded as an elementary excitantion of the dirty
superconductor. An analogy has been drawn with a vortex in Coulomb-blockaded
Josephson junction arrays where a vortex has no core and could have zero
energy. This suggestion is however different from earlier works and
hypotheses concerning dirty superconducting films and Josephson junction
arrays where the possibility of quantum tunneling of already created
Abrikosov vortices has been considered.

Lev Ioffe has outlined his many-body numerical simulations that lead him to
an estimate of phase-slip amplitude in InOx while using a few-site lattice
model. He also suggested that the phase-slip amplitude can be dominated just
by a single optimal path somewhere in the wire, this being in agreement with
other suggestions that weak links can determine the actual magnitude. Such
assumption may aslo explain why the charged impurities do not significantly
reduced the phase-slip amplitude.

It has been noted that the observation of Astafiev is very encouraging for
nanostructuring of the wires to produce more controllable phase-slip devices
where the Coulomb blockade effect can be readily and inambiguosly observed.
The simplest suggestion would be to make two constrictions in the wire
corresponding to two weak links.

It looks like that the report of Astafiev has moved the focus of attention
from the material-science issues to more practical questions. While it
remains to be seen if phase-slips can be observed in traditional candidate
materials like NbSi, TiN, MoGe; InO seems to work. Nano-fabrication and
nano-desing of InO-based devices will probably absorb the attention of
experimentalis for years coming.

Prepared by Yuli Nazarov

Vladimir Kravtsov: Electron cooling rate in amorphous films near superconducting-insulating transition

What can we learn from the giant I-V jumps experiments?

The talk presented overwiev of the work made in collaboration with B.L. Altshuler, V.E. Kravtsov, I.V. Lerner, I.L. Aleiner in response for experimental
findings of M. Ovadia, B. Sacépé, and D. Shahar. The experiment has demonstrated a set of hysteretic I-V curves with order-of magnitude jumps and spectacular temperature dependence. It turned out in 2008 that these curves in all details can be explained if electron overheating is taken into account.

An ultimately simple and elegant phenomenological theory is based on a single equation:
IV= joule heating = cooling rate of electrons to phonon bath, and takes as input the linear temperature-dependent resistance R(Te). The speaker outlined the details of the theory demonstrating its sensitivity to the assumptions concerning the temperature dependence of the resistance and cooling rate presenting several simple solution. Further, he concentrated on the coolest part of the story: temperature-dependent electron cooling rate!

He mentioned that the experimental evidence of strong decoupling of electrons and phonons in insulators undermines usual assumptions that the phonon-assistant electron hopping is the dominant transport mechanism in insulators. The temperature dependence extracted from the experimental data clearly demonstrates the rate proportional to T^6 at hight magnetic fields. T^6 law has been derived for common metals yet by Albert Schmid in seventies. It is somehow puzzling that the proportionality coefficient is 2-4-5 orders magnitude larger than the theory of common metal would predict if extended to localized states (the precise number of orders of magnitudes depends on the estimations of sound velocity). The computation of the coefficient for localized states requires more attention but the power law seem to hold: the speaker argued that the fact that the electron states are localized should not by itself lead to Arrhenius law in temperature dependence.

The most dramatic part of the talk concerned the cooling rate extracted from yet
unpublished data at low magnetic fields. The data did display Arrehius law with energy gap of 1.75 K. The speaker argued that this is a clear manifestation of preformed localized electron pairs in the material. He outlined general problems with forming such pairs in insulator if Coulomb interaction is taken into account. He made use of analogy with double-ionization to assure himself and the audience that Nature permits such things.

The talk provoked a discussion that has started slowly but soon become overheated and
involved multiple parties. Sasha Finkelstein has asked a question about phonon-assistant hoping and expressed his surprise with low energy scale invloved
that is in apparent contradiction with Coulomb energy estimations. The blogger wondered why the cooling rate was assumed to be such a simple function of two temperatures. The answer was that this form was obtained yet by Schmid but eventually
has no apparent reason to be general. Misha Gershezon has shared his experience in measuring colling rates and posed a series of questions addressed to experimentalists and concerned with time scales of cooling. Zvi Ovadyahu mentioned that overheating bistability is readily observed at room temperature. Why does one have to go to low temperatures? The answer: to get cooling rate at low temperatures.

The discussions in groups have lasted at least half an hour after the talk.

Blogged by Yuli Nazarov

Mikhail Feigelman: Fractal and Pseudopgaped Superconductors

Related references: (1) Feigelman et al Phys Rev Lett. 98, 027001(2007); (2) Feigelman et al Annals of Physics 325, 1368 (2010)

Main ingredients of their theory: study competition between Cooper pairing and localization (in the absence of Coulomb interations). In a BCS superconductor coherence lengths are much larger than the lattice constant so need an analytical theory to complement other numerical approaches.

Using Anderson’s pairing of exact eigenstates, they obtain the gap equation which relates the local pairing amplitude at r to the local pairing amplitude at r’ through a non-local kernel K(r,r’). The structure of the kernel is determined by the eigenstates of the single particle wave function that includes only the disorder potential.

Misha and collaborators claim that at the superconductor-insulator transition, the fractal nature of the non-interacting single particle states is important. There are strong local order parameter fluctuations and the region with finite pairing amplitude occupies only a small fraction of the total volume near the transition. Their central result relates the mean field transition temperature to the fractal dimension.

This mean field Tc can exceed the BCS value in the clean system. Note that a similar result was already predicted in our paper Ghosal et al PRB 65, 014501 (2011) (See Eq. 16 and Fig 5) using the same pairing of exact eigenstates as well as Bogoliubov de Gennes methods). Feigelman and collaborators have extended that analysis for a situation where the fractal nature of the eigenstates may be important. They have also pointed out that off-diagonal correlations between the different eigenstates could be important.

I list some points raised during and after the talk but related to this talk :

(1) There have been several assertions of Tc being enhanced by disorder (see also papers by Kravtsov and Mirlin). It is important to distinguish the mean field Tc that these authors as well as Feigelman are talking about from the actual Tc that is dominated by phase fluctuations and I believe monotonically decreases with disorder.

(2) Is the fractal nature of the single particle wave functions that is important near the Anderson transition relavant for the superconductor-insulator transition that occurs at a different critical disorder? This difference is rather stark in 2D where MIT occurs at arbitrarily small disorder but the SIT is moved off to a finite value.

(3) Misha also mentioned pseudogap and parity gap but their definitions were not entirely clear to me. The standard definition of the pseudogap is a suppression in the density of states between the actual transition temperature Tc (defined by where long range coherence sets in) and T* (a pairing scale or a mean field scale). Since the authors only calculated a mean field scale it is not clear how they could have accessed the pseudogap region in these calculations.

Blogged by Nandini Trivedi

Maoz Ovadia: The insulating state in amorphous strongly disordered superconductors

The speaker, Maoz Ovadia, presented the basic facts about InOx superconductors obtained from transport measurements by the group of Prof. D. Shahar at the Weizmann Institute (Israel).

After an obligatory introduction consisting of: (1) the list of theoretical papers by Matthew Fisher et al about the superconductor-insulator transition treated as a quantum phase transition, and (2) comparison of the two standard sets of data obtained in amorphous and granular superconductors, the speaker demonstrated two sets of r(B)-curves (dependence of the resistance on the magnetic field ) in InOx. One set was for a relatively clean superconducting film, and the other set for a disordered one. Resistance at different temperatures exhibits maximum and, consequently, the curves r(B) intersect with each other at some region of the magnetic fields. In the clean film it occurs around 11Tesla. This set apparently cannot be considered as an illustration of a quantum phase transition. An interesting feature of this plot (which was not discussed, unfortunately) is a noticeable resistance in the fields about 1-2 Tesla or less without a clear transition into a superconducting state. This plot was contrasted with the data in a more disordered conductor. There, the curves intersect accurately enough at the magnetic field B* about 2.7 Tesla, i.e., at noticeably smaller magnetic field comparing to the clean case. With the lowering of temperature, curves at fields smaller than B* go down (superconductor) while at the fields exceeding the critical go up (insulator). The speaker demonstrated a curve at T=0.02K which was almost rectangular with the resistance shooting abruptly up to MegaOhms for B> B*, i.e., for magnetic fields on the insulating side of the transition. Thus, one indeed may speak about a quantum phase transition (we put aside the question about how universal is the value of the resistance at the point of the intersection in different films; it is not). The phenomenon is not unique for InOx films, but was also observed by other groups in different materials. However, it was not so pronounced as in InOx.

Interestingly enough, the insulating behavior is limited to a finite interval of magnetic fields. At large enough magnetic fields, the reentrance has been observed; resistance starts to fall down when the magnetic field increases. The whole phenomenon, shooting up to MegaOhms and retracing back to the resistance about 10^4Ohm, develops within the interval of magnetic fields from 2 to 10 Tesla. To get a clue about the origin of the phenomenon, the speaker demonstrated resistance as a function of temperature at a fixed magnetic field (about 5 Tesla). They found an activation behavior with a gap comparable with the superconducting gap in this material.

As another hint, the speaker used the experiment by James Valles’ group, where they observed a sort of Little-Parks oscillations with a period corresponding to a superconducting flux quantum per unit cell in an insulating Nano-Honey-Comb film. The speaker interpreted his data as a random array of tunneling junctions, and the effect of the magnetic field was interpreted as a flux-related effect. A few slides from the paper of Dubi, Meir and Avishai illustrated this point of view. (One may guess about how to reconcile the picture of random tunneling junctions with the results of the STM measurements in this material. In other words, why people have to develop a theory of the preformed pairs, if everything can be explained in such, rather conventional, way?)
Then the speaker switched gear, entirely: he discussed the nonlinear transport in InOx at low temperatures, about 0.1mK. There is a hysteresis phenomenon as a function of bias voltage. First, the data at a high magnetic field of 11Tesla were presented. There is a striking similarity with the data in YSi by M. Sanquer et al. A comparison with the theory of the overheating by Altshuler et al published in PRL 2009 has been discussed. As a justification of this picture (it assumes that resistance depends solely on the electron temperature despite that the transport may be either phonon- or electron-assisted), a paper by Marnieros et al PRL 2000 has been quoted. If not to pay attention on the significant disagreement in a numerical prefactor, the comparison of the data at B=11Tesla with the theory is rather convincing. For B=5Tesla the situation is less satisfactory and it requests a modification of the rate of the electron-phonon scattering (at least).

Since the talk consisted of two disconnected parts, it was difficult to make a certain conclusion. The speaker just thanked the audience for the attention.

Blogger Alexander Finkel’stein

Alexandre Pourret: Nernst signal generated by superconducting fluctuations in low-Tc disordered superconductors

Dr. Pourret presented Nernst Effect measurements as a probe of novel
phenomena in superconductors. He started with a review of a definition of
the Nernst coefficient, which measures the size of a transverse electric
field generated by a longitudinal temperature gradient in a magnetic field.
He pointed out that simple transport theory indicates that the Nernst effect
is proportional to the derivative of the Hall angle with respect to changes
in the Fermi energy. This dependence leads to the so-called Sondheimer
cancellation of the Nernst effect in simple 1 band metals. He went on to
say that non-superconducting materials with a large ratio of mobility to
Fermi energy display the largest Nernst effect.

Next, Dr. Pourret turned to Nernst effect measurements in superconductors.
He characterized the work by Ong's group as a breakthrough in the use of the
Nernst effect to probe novel phenomena in superconductors. That group
observed large Nernst coefficients above the transition temperature in high
Tc materials in the pseudogap regime. The observations have been taken to
indicate the presence of superconducting fluctuations well above Tc. With
those experiments in mind, he and coworkers embarked on Nernst effect
measurements on disordered superconducting films. The high sheet resistance
NbxSi1-x and Indium Oxide films they employed were expected to exhibit large
fluctuation effects.

The experimental results on the NbSi and Indium Oxide films were:

In NbSi, the Nernst coefficient above Tc is much smaller than that below
Tc. The maximum in the Nernst signal exhibited a cusp in a magnetic field
vs. temperature plane, going to zero at Tc. He compared the Nernst
coefficient behavior to a theory labelled USH that gave agreement over a
range of magnetic field. An improved theory fit their data over almost the
entire range.

In Indium Oxide, the Nernst signal decreased with decreasing temperature and
passed smoothly across Tc on cooling. It exhibited no cusp structure.
Thus, there seemed to be no difference between the amplitude fluctuation and
vortex regimes as seen by the Nernst effect. Armitage queried whether the
experiments might show a difference at lower temperatures than those
investigated.

Blogged by Jim Valles

Discussion-session II report: Electrodynamics in strongly disordered superconductors

Suggested questions:

1. how and in what sense would one modify the standard Mattis-Bardeen treatment if applied to highly resistive superconductors.
2. how would one treat a possibly occurring nonlinear response (i.e. power dependence)

Additional questions raised:

· What are the sources of dissipation at frequencies much below the gap in highly disordered superconductors?

Status of the field:

1. Spectroscopy ongoing from 100 MHz to 20 GHz to determine the electronic properties of disordered materials, in particular InOx. All in the small signal limit and across the SIT.

2. User-driven experiments with superconducting resonators of TiN or NbTiN, with a preference for high resistivity but still about a factor of 10 off from the SIT. Signatures that standard Mattis-Bardeen works relatively well but deviations are being identified.

3. There is no specific theory yet for the electrodynamics of disordered superconductors, in view of the fact that the theory to understand the system as such is still under development.

Various remarks:

1. Roughly speaking one might characterize that superconducting state as consisting of percolating inductances, whereas the insulating state is more like percolating capacitors.

2. The non-linear regime is probably determined by Josephson weak links

3. Pump-probe experiments with microwaves might be illuminating to probe the nonlinear regime.

4. Nontrivial sources of dissipation may exist in superconductors with inhomogeneous superfluid density. In general, for resonator applications then, one wants to have highly resistive superconductors, which do not develop significant inhomogeneities.

Prepared by Teun Klapwijk and Peter Armitage

Nandini Trivedi: Single- and two-particle energy gaps across the disorder-driven superconductor-insulator transition

Nandini Trivedi presented results of numerical studies of strongly disordered superconductors and superconductor-insulator transition in 2D lattice case. She starts from general discussion of amplitude fluctuations versus phase fluctuations in presence of disorder, and then she compare two basic energy scales which can be defined : single-particle gap Δ in the electron spectrum, and superfluid density ρ_sThe point is that usually in disordered superconductors ρ_s >> Δ (by orders of magnitude) and thus phase fluctuations are irrelevant apart from the region close to T_c Situation changes upon increase of disorder which leads to strong suppression of superfluid density, which eventually becomes comparable to Δ , since its value is much less sensitive to disorder. It is this region there S-I transition occurs.

Going to quantitative discussion, Nandini defines the Hamiltonian to be used, which isattractive Hubbard model with disorder, defined on 2D lattice. The major part of results was obtained for the attraction coupling constant U close in magnitude to the hopping amplitude t (in other terms, U was about ¼ of the full bandwidth). The restriction of U ~ t instead of U << t (which would better correspond to a real superconductor) is due to limited size of a system which can be studied numerically.

Two different methods were used. One of them is a kind of mean-field theory + Hartree-Fock corrections, implemented on the top of exactly determined single-electron wavefunctions. This method disregards phase fluctuations, the results are mainly presented in previous publications (Phys. Rev. Lett. 1998 and Phys.Rev. B 2001). A new recently developed method, which is the main tool of the presented work was called “Detrimental quantum Monte Carlo”, which is “exact” in the sense that no fluctuations are excluded, and also it does not suffer from usual “sign problem”. The outcome of Monte Carlo simulation gives correlation functions defined in imaginary (Matsubara) time. Then one needs to make analytic continuation to real time domain, in order to get observed spectral functions. “Maximum entropy” method was devised for this analytical continuation. Sum rule was controlled individually at each site on the lattice.

It was observed that pairing amplitude Δ(R) developed emergent inhomogenities at the spatial scale much longer than atomic scale where random potential was originally defined. Simultaneously, single-particle spectral gap was determined locally in space. It occurs that local pairing amplitude Δ(R) and local single-particle gap ω₁ anti-correlates in space: the regions with large Δ(R) usually show smaller ω₁.

Distribution of coherence peak heights P(h) was studied at different temperatures. Whereas at T=0.1 Tc maximum of P(h) is at relatively large h, it is shifted to h=0 at T=0.5 Tc where most of the peaks disappear. In presence of sufficiently strong disorder single-particle gap is suppressed already above Tc, this suppression is seen up to higher temperature T* which is associated with “pseudogap”. The value of T* grows with increasing disorder, whereas Tc drops down. At low temperatures hard gap still exists at strong disorder, where coherence peaks are totally gone. Fully developed gap never was seen right at Tc, contrary to the STM experimental data on InOx (reported by Benjamin Sacepe).

Dynamic current-current correlation functions were extracted from Monte-Carlo simulation

and superfluid density ρ_s was obtained at different degrees of disorder. S-I transition was found as a point where ρ_s vanishes.

Dynamic pair susceptibility χ_pair(ω) was also determined from Monte Carlo simulations plus analytic continuation; it was found that has a spectral gap in the insulating state, which vanishes smoothly at the critical disorder. There is a single value of the critical disorder, that separates superconductive state with nonzero Tc from insulating state with nonzero two-particle gap, whereas single-particle gap stays large throughout the whole quantum-critical region. These findings are in qualitative agreement with results of the analytical theory developed previously by M. Feigel’man, L. Ioffe and M. Mezard (Phys. Rev. B 82, 184534 (2010)). This paper is apparently unknown to Nandini, which makes qualitative agreement between the results even more valuable.

Blogged by Mikhail Feigel’man (Landau Institute)

Claude Chapelier: Very Low Temperature STM: a powerful probe for inhomogeneous superconducting states (tutorial)

Professor Chapelier begins the tutorial by announcing a shift or a theme
that he'd be returning to throughout the talk regarding the question posed,
presumably by the organizers, for the discussion section to happen later
today: "How can one distinguish atomic and electronic inhomogeneities in
real materials?" (paraphrased). The speaker admits not understanding the
question or whether it is one that can be answered and has tried to examine
the field with this question in mind.

His tutorial is organized in three parts, the last of which is a discussion
with questions expanding on the proposed discussion question (above). The
first two parts are I. STM/STS review and II. Applications to highly
disordered superconductors.

Part I. STM/STS review

An STM consists of a metallic tip on a piezo electric tube that allows for
very fine manipulation of the tip near the surface of a sample. A bias is
applied between the sample and the tip, which creates a tunneling current
through the vacuum from sample to tip (or vice versa). The experimenter
measures this tunneling current. Difficulties in low temperature are
related to vibrations. The speaker specifically mentioned the difficulty in
having a high resolution over large (micon) areas because of stronger
vibrations experienced when the piezo is able to scan large areas.

Now we look at some "textbook systems." The first is NbSe2. Where we see
atomic resolution in the microscopy images with an overlaying modulation.
Charge density wave or artifact? Modulation depends on applied bias. Need to
study this superstructure carefully and know things about the tip, like that
its DOS doesn't change with bias.

The slide is interrupted by a computer problem. The speaker claims that the
problem is not on his computer. The organizer accuses the speaker of
stealing a computer. A few cable switches and we're up again.

Now the DOS is studied locally through the IV curves at different spatial
locations on the sample. (Microscopy is done at a fixed V). A kink in the
DOS at the edge of the superconducting gap turns out to be important and was
studied in detail by Guillam (PRB 2008). The kink is more pronounced between
Se atoms. Back to the question regarding different levels of inhomogeneity:
which kind(s) of inhomogeneity are the superstructure and the kink related
to? Blogger doesn't think this question is answered here.

Speaker describes using STM to measure the vortex lattice in
superconductors. References Hess, PRL 1989. The experimenter sits at a bias
voltage that corresponds to the tip of the coherence peak in the
superconductor, then watches coherence disappear periodically with the
spatial scan, revealing an array of vortices in a triangular lattice.

Blogger interprets the discussion to indicate that NbSe2 is especially
well-suited to measuring the vortex lattice. Measurements in BSCCO show much
less contrast between vortex cores and superconducting lattice. A
checkerboard pattern also appears inside the vortex core (which
inhomogeneity is this pattern due to?). (Hoffman data)

The last "textbook system" described is hybrid nanostructures of, for
example, Au overlapping Nb. Experimenters (Vinet, LeSuer) have probed the
DOS spectra at different positions and found a lot of different kinds of
spectra. The behavior of the gap and the coherence peaks appears to be very
complicated, but may also be well understood (?).

Part II. Highly disordered Superconductors

The disorder-driven SITs of granular films are compared to those of
homogeneous films. Homogeneous SITs have a sharp transition where insulators
give way directly to superconductors whereas granular SITs show more
features near the transition, like reentrance and kinks in the R(T).

Next, the disorder driven SIT of sputtered TiN films is shown, and shows
similarities to both the homogeneous and granular SITs previously shown. The
question of whether these films are granularly or homogeneously disordered
motivates the STM experiments.

STM measurements show superconducting grains embedded in an insulating
material. The spectra in a line across the grain edge shows a nice gap in
the superconductor that fills in with shrinking coherence peaks as you move
into the insulator. Curiously the gap width does not change. This does not
seem to be understood.

TiN films made by Atomic Layer Deposition (a la Baturina) seem to be a
totally different story. These films have very small nano-crystalline
grains, but are homogeneously disordered within the grain. Tc changes with
disorder in a way that roughly matches predictions of Finkelstein's model.
Additionally, the spectral measurements fits BCS rather well at low T and
low bias. However, these spectrum are not spatially homogeneous and vary
quite a lot from place to place (for ~100nm distances).

Some similarities are drawn to Trivedi's work: Tc goes to zero before the
gap disappears with increasing disorder. Also, something of a gap persists
far above Tc. Can plot this 'anomalous conductance' (at zero bias) with
temperature and find deltaG/G~ln(T/Tc), which the blogger understood to be
consistent with predictions due to superconducting fluctuations from
Varlamov and Dorin, JETP 1983 (not familiar with this work). Deciding
carefully on Tc to the accuracy of <50mK is important to getting this linear
dependence. Experimentally, Tc is very close to R(T)-->0.

This analysis brings up a conundrum, between microscopic (superconducting
fluctuations) and macroscopic (Tc) quantities which the blogger did not
completely understand.

Part III.

The speaker repeats the discussion question about atomic versus electronic
inhomogeneities. It seems no one wants to supply an answer as the audience
questions are all unrelated. Perhaps it will be addressed in tomorrow's
discussion section.

Blogged by Shawna Hollen (Brown)

Pratap Raychaudhuri: Phase fluctuations in 2D and 3D NbN thin films

Pratap Raychaudhuri gave a beautiful talk on their very systematic and complete measurements on various properties of NbN films. He started by reminding us that low superfluid density superconductors may have phase transitions which are driven by fluctuations of the superconductor's order parameter's phase. These fluctuations are largely irrelevant for conventional superconductors where the "phase stiffness" is 10^7 K. The phase stiffness is the energy scale to put twists in the superconducting phase. In highly disordered systems or in systems where otherwise the superfluid density is low, the stiffness can be of order T_c.

Their material of choice is NbN, which is claimed to be a garden variety type II crystalline superconductor. They sputter epitaxial films and although films are largely crystalline, they can control defects and hence disorder in the materials by controlling the ratio of Nb to N2 in the plasma.

Pratap then gave us a brief review of the physics of the KTB transition. He reminded us about universal jump of the superfluid density in which there is a discontinuous jump of the superfluid density of an amount set by the transition temperature itself.

They measure superfluid density (or phase stiffness) that they parametrize by inverse penetration depth squared. They observe that in thin nominally 2D films the inverse penetration depth shows a substantial downturn in the rough vicinity of the KTB expectation, although the downturn has a magnitude is systematically less than T_KTB. They perform a detailed fitting based on a model which takes into account the finite vortex energy and a small distribution in superfluid densities and get energies of order the expectation for vortex core energies of order the expectation for 2DXY model.

Pratap then moved to samples which are more 3D. They get k_Fl from Hall and DC resistivity measurements. They find that T_c goes to zero around the disorder level where kFl approaches 1, which is essentially indistinguishable from the disorder level where the normal state conductivity is going to zero. i.e. the MIT is coincident with the SIT.

Pratap then discussed their STM results. He showed line scans on a variety of films. For instance on low disorder film the sample shows a large BCS-like gap which don't depend on position and opens up at T_c. He then showed data from more disordered samples. These samples show an onset in superconducting features in the tunneling spectra above T_c. For the particular sample he concentrated on T_c was ~2.5 K and his T* was 7-8K.


Then he showed a phase diagram as a function of k_Fl. For high k_Fl, T* and T_c coincide, but as k_Fl approaches 1, then T* and T_c separate and there is a substantial pseudogap (PG) regime. This is the same regime where T_c is suppressed to zero. He then asked if it was reasonable to assume that in this regime the transition was driven by phase fluctuations. To answer this question, he then presented their penetration depth data which was taken on these same samples. On the samples with a substantial PG the phase stiffness is of order T_c.

In the last part of the talk he analyzed the BCS prediction for the phase stiffness for samples with these T_c's (Blogger: same spectral weight in the superconducting condensate). He showed that for highly disordered samples the phase stiffness was systematically less than the BCS expectation. He attributed this to quantum fluctuations of the superconducting phase.

In the future, they want to look for low energy dissipative modes (which derive in their interpretation from quantum fluctuations) via microwave measurements. In the tunneling spectra they see low energy in-gap states for highly disordered samples and Pratap mentioned that perhaps these were the low energy modes. (It was not clear to the blogger how this was relevant, as tunneling measures single particle excitations and presumably these modes are not single particle excitations.).

As one final final point, he mentioned that for 3D samples which were just barely disordered enough not to be superconducting, they see a large magnetoresistance peak as has been see in materials ilk TiN and InO. He interpreted this peak as the delocalization of Cooper pairs.

In the questions, the blogger pointed out that one could get a depleted condensate density (lower phase stffness) by inhomogeneous superfluid density alone. Then by arguments of spectral weight conservation one must have finite omega plasmon-like modes. These are purely classical (or at least not necessarily quantum) and so are really a different effect than the one Pratap discussed, but in principle could also explain his data.

Blogged by Peter Armitage

Zvi Ovadyahu: Field-enhanced conductivity in electron-glasses

Zvi Ovadyahu reported on the absorption rate in strongly localized Anderson insulators.

The bottom line message of the talk was to provide evidence that the electron-electron inelastic scattering rate in Anderson insulators is strongly suppressed from its value in the less disordered, diffusive regime. This may be an indication of the physics of many-particle localization in strongly disordered systems.

The material under investigation was InOx, one of the standard materials in which electron glassiness is studied. An electron glass is an Anderson insulator where all relevant single particle states are localized. Coulomb interactions are very important due to the absence of standard screening. Thus there are strong and long ranged interactions, as far as screening due to gates or thermal excitations can be neglected. The frustration between disorder and Coulomb interactions produces a glassy state.

All samples studied for the present purpose were 2d, crystalline In2O{3-x} films, measured at 4K where they are in the hopping regime (resistances ~10 MOhm). This specific variety of InOx was chosen because all its parameters are known, being close to a free electron system (unlike the amorphous systems).

The basic glassy or out-of-equilibrium phenomenon in InOx is the slow logarithmic relaxation of conductance with time after a quench from high T. Other ways to excite the system include non-Ohmic fields, or raising the bath temperature, both of which make the conductance quickly jump upwards, and then slowly increase further. Upon undoing the perturbation the conductance jumps down and relaxes back logarithmically towards the previous state. Both excitations have qualitatively similar effects.

The system was excited with non-Ohmic fields of various frequencies, to pump energy into the system. Thereby the power was adjusted in such a way as to keep the initial jump of conductance constant. The frequency range covered 23 Hz up to15.5 MHz.

A first interesting result concerns the apparent energy, as a proxy for which the initial conductance after the downjump is taken. Apparently, the absorbed energy depends on the frequency: it starts decreasing for frequencies of order 10^5 Hz and higher. The meaning of this characteristic scale frequency was not explored further here.

The focus of the talk was rather on the rate of e-e inelastic processes. An upper bound for the latter was obtained by considering the heat balance in the steady state under non-Ohmic excitation. This allows to obtain a good estimate of the heat removal rate from the electrons. Ovadyahu argues that in the steady state, it must be an upper bound on the inelastic collision rate, which controls absorption (otherwise the system would absorb more energy and come to a steady state with higher heat removal rate). His finding is that the inelastic rate in the insulator is as small as gamma= 3.5*10^5 Hz, as compared to measured rates of the order of 10^11/s in the diffusive regime.

The large difference must almost inevitably be blamed on localization and the associated discreteness in the insulator (the single particle level spacing is 100-10^4 K!). From this point of view the experiments seem to be consistent with tendencies expected in systems featuring manybody localization, as proposed by Basko et al.. Remarkably, the (near) discreteness seems to hold despite the presence of strong, long range interactions, which are in principle expected to destroy the discreteness of the spectrum and delocalize the many body excitations (see, Fleishman and Anderson).

A possible element of an explanation may be that these excitations are indeed delocalized, but have a very low diffusivity because dipolar interactions in 3d are only marginally long range which is the case of critical hopping, discussed in Anderson '58.

Blogged by Markus Mueller

Jian-ting Ye: Liquid-gated interface superconductivity on an atomically flat film

Jian-ting Ye discussed their recent beautiful work from Tokyo on gating various materials to induce superconductivity (and other states of matter) using ionic and organic electrolyte solutions. They make an electronic double layer transistor (EDLT) with liquid gating. Much more charge is introduced as compared to conventional SiO2 style dielectrics.

Jiang-ting discussed a large number of results using this technique. With polymer electrolyte solutions, they have found a 2D metal-insulator transition in ZnO. (As a practical matter, states induced by this method will generally be 2D) For smooth changes of voltage, there is a sudden onset in resistance when resistance gets near h/e^2. They have also induced superconductivity in StTiO3 around 0.4K, which is a similar temperature to that found recently in STO/LaAlO3 superlattices. Capacitance is high enough that for materials like graphene they can see particular bands crossing the Fermi level in the case of graphene.

To get larger charge densities they use ionic liquids where they get get ~ 20 times higher charge density than with polymer electrolytes. They have looked at many layered structures (cuprate superconductors, layered chalcogenide topological insulators, layered chalcogenide superconductors, etc.) and found a number of effects. But in the rest of talk will talk he was going to emphasize their work on superconductors.

ZrNCl was induced to be a superconductor at 15.2K with Tc's very similar to what is found when this material is doped with Li.

Transition metal chalcogenide MoS2 when electron doped with the EDLT technique is found to have superconductivity at 9K. This is higher than the previous record of about 6.5K when this system is doped with alkali metals. They also find ambipolar conductivity for positive and negative bias in this system, but no ambipolar superconductivity yet.

It was asked by Finkelstein why it is that there is is no problem with mobility in these systems, in the sense that in 2D electron glass in semiconductor heterostructures, dopant layers reduce mobilities. Why does not this not happen here? The speaker replied that they are in a different regime with regard to the range of mobilities. Here mobilities are in the 100's at best, whereas the best 2DEG have mobilities 10^4.

Blogged by N. Peter Armitage

Jim Valles: Insulator to superconductor transitions come in multiple flavors in quench condensed films

Jim Valles describes that superconductor to insulators transitions (SIT) come in 3 flavors in quenched condensed films: granular, uniform and nano-honecomb (NHC) structures. The NHC films usually have the thickness about the same as the uniform ones and the variation in their thickness is about a couple of angstroms.

Jim Valles discussed the possible ways to kill the superconducting order parameter through SIT. In weakly localized system, the transition happens in an amplitude reduction fashion and cooper pairs (CPs) are de-paired. Another way to kill superconductivity is phase fluctuation which leads to localized CPs. In granular films, quasi-particle (qp) tunneling dominates while for NHC films, CPs tunneling takes charge.

For quenched condensed Bi films, with a-Sb underlayer, those films on glass or AAO (honeycomb structure) substrates are homogeneous, while the films are granular when the underlayer is missing. Most of the Bi measurements have to be done in situ.

He explained how resistance evolves in granular films through SIT and those films tend not to be conducting unless one has 2 layers of grains. Granular films usually have localized CPs and phase fluctuations near SIT. The transport effects are dominated by interisland qp tunneling. He showed data for granular lead which has giant negative magnetoresistance(MR) and can be fitted to SIS model with magnetic field induced pair-breaking.

For uniform amorphous Bi film, he thinks they are in the Fermi insulator phase. For weak insulating normal state, the change in conductance is proportional to log(T). They have positive but not large MR. Superconducting gap also disappears near SIT and the energy gap can be fit roughly with BCS form. Reference Valles, Dynes, Garno PRL 1992.

For NHC Bi films, perpendicular penetration length is about 1 mm and coherence length is about 10 to 20 nm. AFM images of this type of samples show “regular” height +variation. Thickness tuned SIT shows re-entrant behavior. NHC insulating films has a hard gap R~R0 e^(T0/T) and the activation energy T0 goes to 0 for thicker films. They exhibit large flux oscillation under perpendicular field and also giant positive MR. Transport measurements are dominated by incoherent CP tunneling. The size of the orbit of CP is dictated by the size of the unit cell. He believes that for NHC Bi films, they have phase fluctuations driven SIT and localized CPs do exist.

He raised a couple of questions about the origin of the activation energy, origin of giant MR, the mechanism causing localized CP in NHC films and also why qp/CP tunneling dominated for granular/NHC films.

He answered some of the above questions by introducing a local Tc0 variation which is caused by thickness variations in NHC films. He mapped out Tc as a function of position near SIT and introduced a weak link model. By including a circuit model, he got R^(link) at the critical point to be R_Q.

Blogged by Wei Liu (JHU)

Claire Marrache-Kikuchi: Thickness, composition and annealing tuned disorder in NbxSi1-x

Claire Marrache Kikuchi gave a detailed presentation on disordered amorphous Nb_xSi_1-x focusing on 3 different ways to control disorder: (i) By tuning the thickness of the sample, (ii) by changing the composition and (iii) through controlled annealing. She started by reminding the audience that different kinds of disorder can have fundamentally different effects. For example, with decreasing thickness surface phonon softening can play an important role and has often been argued to be the reason for enhancement of T_c in observed in Al and Sn. In addition, she reminded the audience, the difference between homogeneous and granular disorder has been highlighted by many authors.

Amorphous thin films of Nb_xSi_1-x were grown through co-deposition of Nb ans Si using electron beam evaporation. For thick films (thickness>50nm) samples with composition 11-18% Nb showed superconductivity. The samples have electronic density of states at Fermi energy in the range 10⁴¹ states/J-cm³ which is comparable to that of Au. TEM images of the samples do not show any granular structure.

The composition tuned samples have a metal-insulator transition at 9.9% of Nb, with samples below this composition range exhibiting Efrot-Schlovsky behavior in their transport properties. Interestingly, in this system superconductivity gets apparently destroyed well inside the metallic regime unlike amorphous InO_x and TiN where superconductivity persists in the disorder driven insulating regime. This point towards a very different mechanism, arising maybe from the increase in e-e interactions resulting from a loss of effective screening, which drives the superconducting transition temperature in this material. However, further measurements down to lower temperatures would be needed to confirm this.

In the composition range where the samples are superconducting (e.g. 14%, 15% and 18%), T_c monotonically decreases with decresing thickness. The dependence of T_c on the sheet resistance is qualitatively consistent with an increase in e-e repulsive interaction resulting from the loss of effective screening. However, there are quantitative discrepancies with theory.

The most intriguing aspect of these samples was the effect of annealing. While there is no discernible change in the morphology with annealing up to 500⁰C, contrary to usual expectation the sheet resistance gradually increases and the T_c decreases with increasing annealing temperatures. There was considerable discussion on the microscopic changes that could be responsible for this behavior. It was felt that this issue needs to be looked into further using other microscopic tools. However, one important point was that T_c evolves in the same way with sheet resistance for both composition driven and annealing driven disordered sample, whereas the thickness tuned samples did not fall on the same curve.

In summary, the well characterized samples of Nb_xSi_1-x would definitely provide us with another system where various scenarios proposed for the superconductor-insulator transition could be compared with experiments. It would be interesting to study these sample with various experimental probes such as STM and penetration depth measurements and compare the commonalities and differences with TiN, NbN and InO_x. Prof. Claude Chapelier mention during the discussion that STM measurements on this system are underway. Hopefully, as more systems get studied, a common picture for the disorder driven SIT in various systems will gradually emerge.

blogged by Pratap Raychaudhuri

Teun Klapwijk: Highly resistive superconducting resonators: why and how

Teun Klapwijk spoke on energy-resolving THz detectors for astrophysical
observations. These frequencies are of interest for learning about the early
universe, some 400 million years ago, where radiation from the first stars
excites nearby dust, which then re-radiates in the THz band (~100-600 micron
wavelength).

Previous cryogenic detectors used for this purpose are TESs, photon-assisted
tunneling devices (SIS junctions), and HEB mixers.
in photon-assisted tunneling detectors, an SIS junction is voltage biased
such that THz photons can create quasiparticles above the gap by direct
absorption. HEB mixers use the self-heating-induced nonlinearity in a
nanoscopic superconducting microbridge to mix THz radiation down to
microwave frequencies. TESs use a very sharp resistive transition in a very
low-Tc material as a thermometer to detect the temperature change of a very
low heat-capacity, well-isolated absorber due to the absorption of single
photons.

TESs are the most advanced of these and have the world-record low
noise-equivalent power of ~10^-20 W/Sqrt[Hz] (Gershenson). This has now
reached the limit associated with the background photons, below which
further increases are less useful.

However, one disadvantage of these detectors is that they are read out with
SQUID amplifiers, which are difficult to read out in extremely large
numbers. The most advanced TES array for this purpose, SCUBA II, has 10000
array elements.

Microwave kinetic-inductance detectors have a possibility to go beyond this
limitation. They are built out of extremely high-Q resonators of disordered
superconducting films, with high kinetic inductance and broadband
absorption. Absorption of a photon generates quasiparticles which both shift
the resonator frequency (due to the modified kinetic inductance) and reduce
the Q (due to additional dissipation). This can be detected my monitoring
the microwaves reflected from the resonator. In addition, many resonators
can be connected to the same feedline in parallel, each with a slightly
different resonance frequency. As the Q is increased, the density of these
frequencies can also be increased, up to the required bandwidth for the
detector elements. This allows many detector elements to be read out on a
single coax, so that very large arrays can be contemplated without requiring
impractically many coaxes.

The figure of merit for an MKID involves several factors. First, the
fraction of the total inductance in the resonator which is kinetic; ideally
this would be 1 for maximum sensitivity, and this suggests the use of very
high kinetic inductance materials and geometries. Second, the quasiparticle
recombination time, which should be as long as possible, such that a given
number of excitations can be measured for maximum time in the resonator.
Third, the resolator Q should be as high as possible, in order to be
sensitive to as small an inductance change as possible. Finally, the
quasiparticle density of states should be as low as possible, for maximum
fraction change in the kinetic inductance for a given number of
quasiparticles.

TiN maximizes these figures of merit in many ways better than any material
previously tried:
- The high sheet resistance corresponds to a very high kinetic inductance,
giving kinetic inductance fractions near unity, and very compact resonators.
- Extremely high Q values up to 2 x 10^7 have been demonstrated at high
power
- The Tc can be continuously tuned by varying the deposition parameters;
this allows low gaps to be used for maximum sensitivity
- The extreme disorder gives very good far-IR absorption
- In spite of the high disorder, the quasiparticle lifetime is still
reasonably long

Blogged by Jamie Kerman

Vincent Bouchiat: Tunable 2D superconductivity in metal-decorated graphene

Bouchiat presented experimental results from recent transport studies on superconductivity in thin metals deposited on top of 2D graphene layers. Gated graphene is used as 2D host material mediating interactions between adsorbed metal islands. These metal islands both efficiently dope the underlying graphene sheet and induce long range superconducting correlations.The fabrication of these systems were done in collaboration with Zettl's group at Berkeley. The dewetting of metals such as Pb, In, Sn when deposited on graphene allows non percolating islands of adsorbates to be formed on graphene with typical sizes of ~ 50 nm with inter-adsorbate distances ~ 80 nm (for Sn). With Sn islands on graphene, a gate-induced superconductor-normal transition was observed. When plotting resistane vs temperature, two drops in R are observed: one at T_c, corresponding to the bulk superconducting transition in the clusters and a second one below T_c, at T_BKT, where vortex unbinding occurs. By tuning the gate voltage and thereby the carrier density in the graphene sheets, it is found that T_c remains constant but T_BKT can be tuned on both the electron and hole branches on either side of the charge neutrality point in graphene.

In the second part of the talk, more disordered graphene layers grown by CVD method is used to study Pb clusters. The interesting results are: (1) Dirac point is found to be an insulating point and (2) superconductivity in found only on one side of the charge neutrality point. A gate-tunable superconductor-insulator transition was observed and the graphene layer was found to act as both Josephson and dissipation channels.

In summary, in clean exfoliated graphene, a gate controlled 2D superconductivity - BKT transition was observed and in disordered CVD grown graphene, a gate-controlled superconductor-insuator transition is observed. Metal decorated graphene appears to be a useful model system to study gate-controlled superconductivity. Some results presented have appeared in Phys. Rev. Lett. 104, 047001 (2010).

Blogged by Sambandamurthy (Buffalo)