Their material of choice is NbN, which is claimed to be a garden variety type II crystalline superconductor. They sputter epitaxial films and although films are largely crystalline, they can control defects and hence disorder in the materials by controlling the ratio of Nb to N2 in the plasma.
Pratap then gave us a brief review of the physics of the KTB transition. He reminded us about universal jump of the superfluid density in which there is a discontinuous jump of the superfluid density of an amount set by the transition temperature itself.
They measure superfluid density (or phase stiffness) that they parametrize by inverse penetration depth squared. They observe that in thin nominally 2D films the inverse penetration depth shows a substantial downturn in the rough vicinity of the KTB expectation, although the downturn has a magnitude is systematically less than T_KTB. They perform a detailed fitting based on a model which takes into account the finite vortex energy and a small distribution in superfluid densities and get energies of order the expectation for vortex core energies of order the expectation for 2DXY model.
Pratap then moved to samples which are more 3D. They get k_Fl from Hall and DC resistivity measurements. They find that T_c goes to zero around the disorder level where kFl approaches 1, which is essentially indistinguishable from the disorder level where the normal state conductivity is going to zero. i.e. the MIT is coincident with the SIT.
Pratap then discussed their STM results. He showed line scans on a variety of films. For instance on low disorder film the sample shows a large BCS-like gap which don't depend on position and opens up at T_c. He then showed data from more disordered samples. These samples show an onset in superconducting features in the tunneling spectra above T_c. For the particular sample he concentrated on T_c was ~2.5 K and his T* was 7-8K.
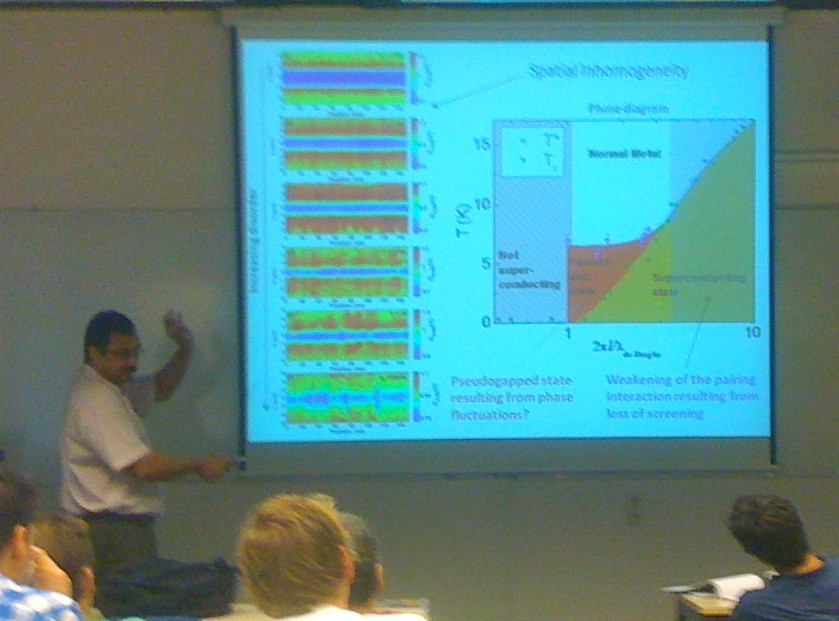
Then he showed a phase diagram as a function of k_Fl. For high k_Fl, T* and T_c coincide, but as k_Fl approaches 1, then T* and T_c separate and there is a substantial pseudogap (PG) regime. This is the same regime where T_c is suppressed to zero. He then asked if it was reasonable to assume that in this regime the transition was driven by phase fluctuations. To answer this question, he then presented their penetration depth data which was taken on these same samples. On the samples with a substantial PG the phase stiffness is of order T_c.
In the last part of the talk he analyzed the BCS prediction for the phase stiffness for samples with these T_c's (Blogger: same spectral weight in the superconducting condensate). He showed that for highly disordered samples the phase stiffness was systematically less than the BCS expectation. He attributed this to quantum fluctuations of the superconducting phase.
In the future, they want to look for low energy dissipative modes (which derive in their interpretation from quantum fluctuations) via microwave measurements. In the tunneling spectra they see low energy in-gap states for highly disordered samples and Pratap mentioned that perhaps these were the low energy modes. (It was not clear to the blogger how this was relevant, as tunneling measures single particle excitations and presumably these modes are not single particle excitations.).
As one final final point, he mentioned that for 3D samples which were just barely disordered enough not to be superconducting, they see a large magnetoresistance peak as has been see in materials ilk TiN and InO. He interpreted this peak as the delocalization of Cooper pairs.
In the questions, the blogger pointed out that one could get a depleted condensate density (lower phase stffness) by inhomogeneous superfluid density alone. Then by arguments of spectral weight conservation one must have finite omega plasmon-like modes. These are purely classical (or at least not necessarily quantum) and so are really a different effect than the one Pratap discussed, but in principle could also explain his data.
Blogged by Peter Armitage
No comments:
Post a Comment